ハノイの塔のアニメーション

ハノイの塔にまつわる伝説

　インドのガンジス河のほとりにある寺院に、ダイヤモンドの針でできた3つの棒が立っている。３本のうちの1本には、64枚の黄金の円盤が積み重ねられている。円盤は、上にいくほど小さくなるように重ねられている。僧侶たちは、そこでずっと円盤を別の柱に移しかえる作業を行っており、すべての円盤を移し終えたとき、この世が終わるとされている。

もちろん、これは作り話ですが、64枚の円盤を移し替えるのに果たしてどのくらいかかるのか、興味のあるところです。

ハノイの塔のルール

ハノイの塔のルールは非常にシンプルです。

1. 積み上げられた円盤をすべて他の棒に移し替えなければならない。
2. 動かすことができる円盤は一度に一枚だけ。
3. 小さな円盤の上に大きな円盤を置いてはならない。（ピラミッド型を維持すること）
4. ３本の棒を必ず使うこと。円盤を他のところに置いてはならない。

ハノイの塔は典型的な自己回帰プログラム

ハノイの塔のアルゴリズムは非常にシンプルです。複雑そうに見えますが、プログラムではわずか数行で書くことができます。

なぜなら、このアルゴリズムは、

の繰り返しに過ぎないからです。マトリョーシカのような構造ともいえます。

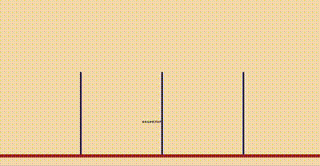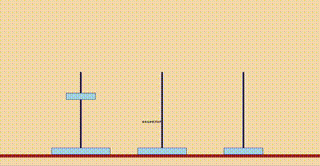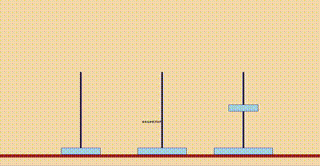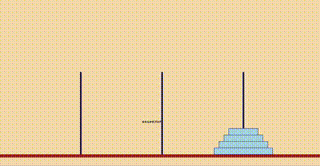
円盤が３枚の場合を考えてみたいと思います。

左端の棒に円盤が3枚重ねられています。この３枚の円盤を右端に移動させます。

そうすると、１番下の円盤を右端に移動させなければなりません。となると、上の２枚は真ん中の棒に移動しておく必要があります。次は、真ん中の２枚の円盤を右端に移動させることになります。ここで、３枚の移動の問題が２枚の移動の問題に変化します。

最後に、一番下の円盤を右端に移動させるために、一番上の円盤は左端に移動させます。

要するに、一番下の円盤を移動させるために、残りの円盤を左端と真ん中の２本の棒を行ったり来たりさせることになります。

結論だけを書くと、円盤を移し替える回数は、円盤の枚数をnとすると、

2ⁿ − 1

という、シンプルな形になります。これは指数関数なので、枚数が増えると回数が急激に増えることになります。

１枚移動させるのに１秒かかるとして、どのくらいの時間がかかるか、ざっと計算すると、以下の表のようになります。64枚になると、もはや永遠ともいえる時間になってしまいます。

戦国時代に、部下が褒美として、将棋盤に最初は1粒、次は2粒と、ひとマスごとに米粒を倍にして欲しいと提案をして、殿様がそのくらいなら、と甘く見ていたら、破産してしまった、という逸話があります。紙をどんどん折り曲げていくと、やがて月にたどり着く、といったように、指数関数がいかに急激に増えるものなのか、実感させられると思います。

枚数n	移し替える回数	時間
1	1	1秒
2	3	3秒
3	7	7秒
5	31	31秒
10	1,023	17分
64	約18,446,744兆	5,849億年