マンデルブロ集合とは?
マンデルブロ集合は、複素平面上の特定の点の集合であり、フラクタルの一種です。マンデルブロ集合は、その美しい形状と自己相似性で知られています。
マンデルブロ集合の生成
マンデルブロ集合は次のように生成されます。
- 各複素数 cについて、初期値 z0=0 を設定します。
- 次の反復操作を行います。この漸化式はジュリア集合と同じです。
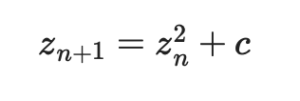
- この操作を無限に続けたときに、znが発散(無限大に近づく)かどうかを調べます。発散するならその点 cはマンデルブロ集合に含まれません。発散しないなら、その点 cはマンデルブロ集合に含まれます。
この反復操作を複素平面上のすべての点 cに対して行い、結果として得られる集合がマンデルブロ集合です。
マンデルブロ集合の特徴
- 複雑な形状: マンデルブロ集合は非常に複雑な形状を持ちます。無限に拡大しても同じようなパターンが現れる自己相似性が特徴です。
- 自己相似性: マンデルブロ集合の各部分は全体の形状と似た構造を持っています。これを自己相似性と呼びます。
- 美しさとカオス: マンデルブロ集合は、非常に美しいフラクタルパターンを持ち、多くの芸術作品のインスピレーションになっています。
マンデルブロ集合の例
マンデルブロ集合の標準的な形状は以下のようになります。


この画像はマンデルブロ集合の一部であり、無限に拡大することができます。拡大しても新しいパターンが現れ、その複雑さに驚かされます。
マンデルブロ集合とジュリア集合の関係
マンデルブロ集合とジュリア集合は、どちらも複素平面上に存在するフラクタルですが、これらの間には深い関係があります。以下に、その関係と違いについてわかりやすく説明します。
マンデルブロ集合とジュリア集合は、どちらも複素関数
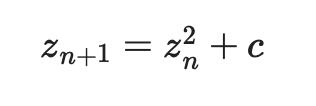
の反復操作に基づいて生成されます。ここで、cは複素数のパラメータです。
1. 定義の違い
- ジュリア集合 (Jc): 固定された複素数 cに対して、反復操作
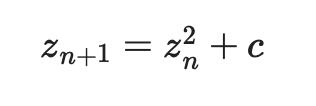
が発散しない点 z0の集合。
- マンデルブロ集合: 初期値 z0=0を固定し、反復操作
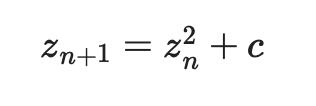
が発散しないような cの集合。
2. 連結性
- ジュリア集の形状はパラメータ cによって大きく変わります。特定の cの値に対して、ジュリア集が連結であるか断片的であるかが決まります。
- マンデルブロ集合内の c: ある c がマンデルブロ集合に含まれている場合、その cに対応するジュリア集 Jcは連結になります。
- マンデルブロ集合外の c: ある c がマンデルブロ集合に含まれていない場合、その cに対応するジュリア集 Jcは離散的(分断された)になります。
