N次魔方陣の縦、横、斜めの和(これを「定和」といいます。)は以下の数式で求められます。
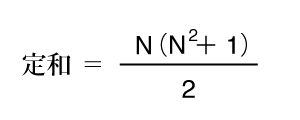
では、実際に確かめてみます。
3次魔方陣 → Nに3を入れると、15になります。
4次魔方陣 → Nに4を入れると、34になります。
確かに公式の通りになります。では、なぜこの公式になるか、考えてみたいと思います。
4次魔方陣を例に考えてみます。aからpには、1から16の数字が重複することなく入ります。

定和をxとすると、行の和はすべて同じになるので(縦で考えてもOK)、
- a + b + c + d = x
- e + f + g + h = x
- I + j + k + l = x
- m + n + o + p = x
この4つの式を合体させると、
a + b + c + d + e + f + g + h + I + j + k + l + m + n + o + p = 4x
となります。
4次の魔法陣なので、aからp二は、1から16までの数字が入りますので、
a + b + c + d + e + f + g + h + I + j + k + l + m + n + o + p
= 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16
となります。つまり、N次魔方陣として一般化すると、
Nx = 1 + 2 + 3 + ・・・ + N2
という等式が成り立つことになります。ここで、自然数の和を求めてみたいと思います。
1 + 2 + 3 + 4 + 5 + 6 +・・・+ n
は、等差数列の和の公式から、
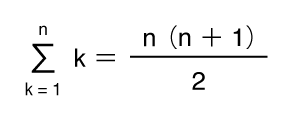
となります。n=2の場合は1+2=3、n=3の場合は1+2+3=6になります。
では、1 + 2 + 3 + ・・・ + N2の合計は、nにN2を代入すればよいので、
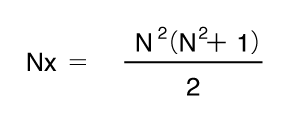
となります。両辺をNで割れば、定和xを算出することができます。
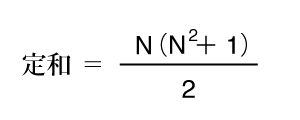
となります。なお、
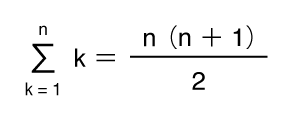
の証明は簡単です。1からnまでの総和xは、
x = 1 + 2 + 3 + ・・・ + (n − 2) +( n − 1) + n
x = n + (n − 1) + (n − 2) + ・・・ + 3 + 2 + 1
二つ目の式は、一つ目の式の右辺をひっくり返しただけですので、同じ式です。ここで、二つの式を合体させてみます。
- 1+n = n+1
- 2+(n − 1)= n+1
- 3+(n − 2)= n+1
という感じで、右辺の各項を単純に足していくと、右辺はn個の(n+1)の和になります。
2x = (n + 1)+(n + 1)+(n + 1)+(n + 1)+(n + 1)+・・・+(n + 1)
= n ×(n + 1)
両辺を2で割ればと上の式になります。
