自然界での生物の個体数を表すモデルとして提示されるのがロジスティック写像です。
「人口論」で知られる、マルサスのモデルの離散型です。
xn+1 = r xn(1-xn)
この極めてシンプルな方程式が非常に複雑な挙動を示します。
バッタやセミなどの個体数変化の理由についても理解が進みます。バッタやセミは数年おきに大発生を繰り返すことで有名ですが、その現象もこのロジスティック写像の解によく現れています。
xnはn世代、xn+1は(n+1)世代の個体数を表します。(n+1)世代の個体数は、n世代の個体数に比例し、またn世代のうち何割かは死んでしまう点をこの方程式は表しています。
rは変数で、このrを変化させると、個体数の変動に複雑な挙動が見られるようになります。
横軸はn、つまり、世代数です。
縦軸は、個体数(便宜的に0から1の範囲に収めるように計算)です。
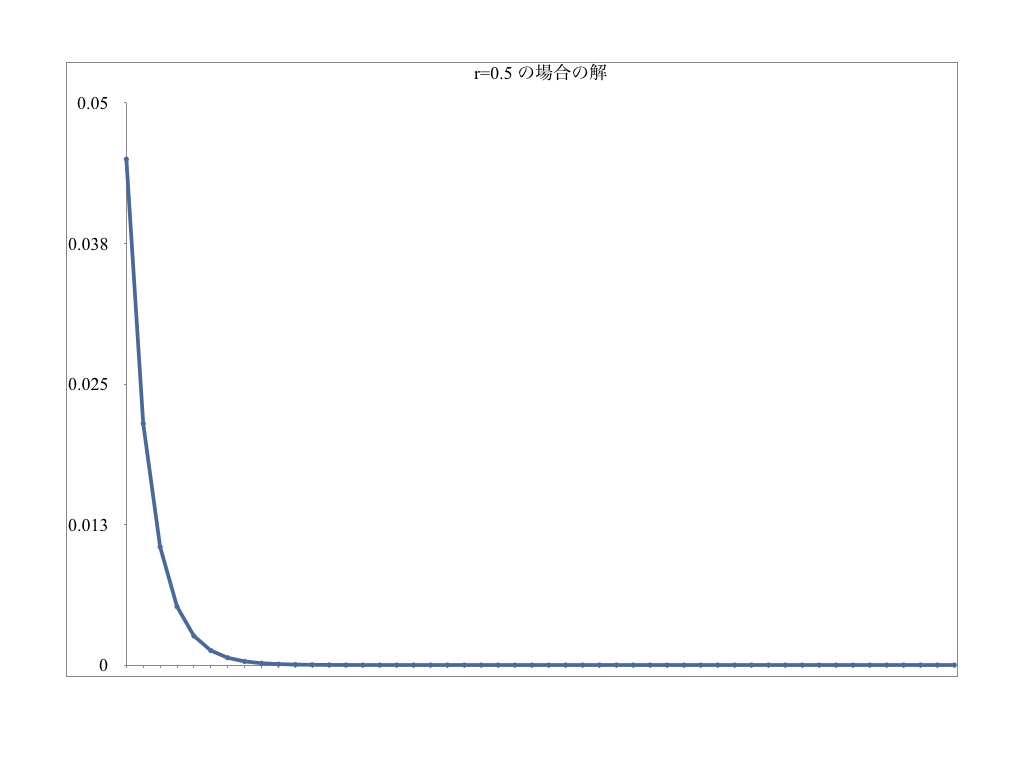
r=0.5の場合は、個体数がゼロになってしまいます。つまり、絶滅ルートです。
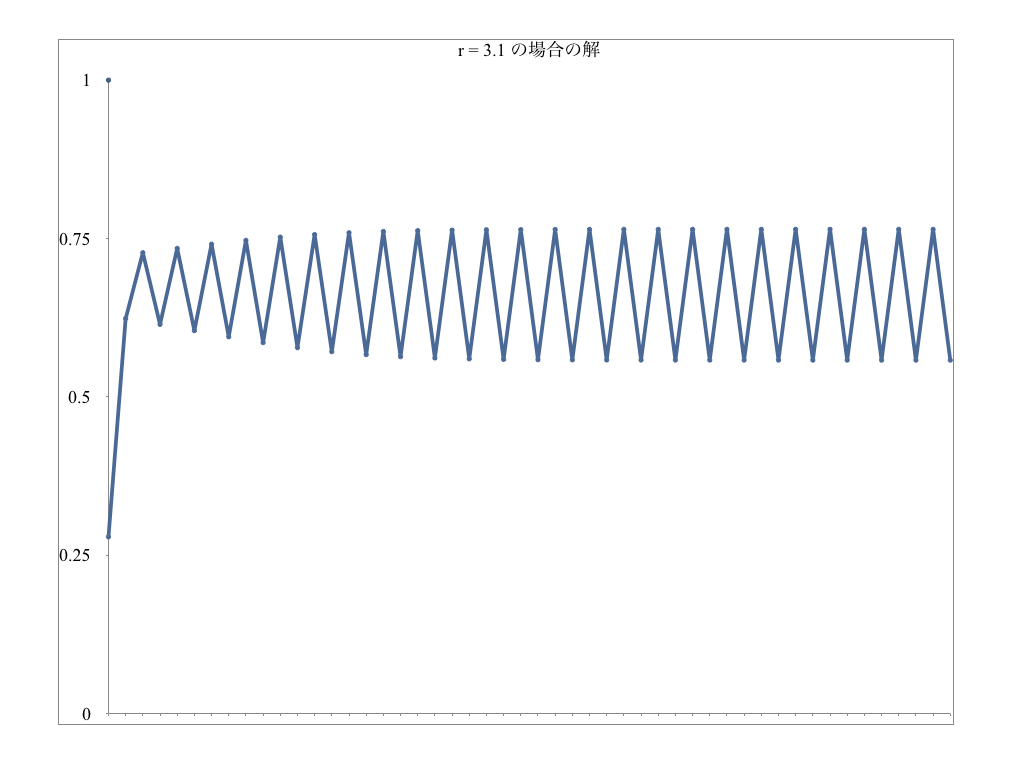
r=3.1の場合は、個体数が増えたり減ったりを繰り返します。食料が増えると個体数が増えますが、個体数が増えすぎると今度は食料難となったり環境が悪化することによって個体数が減ります。
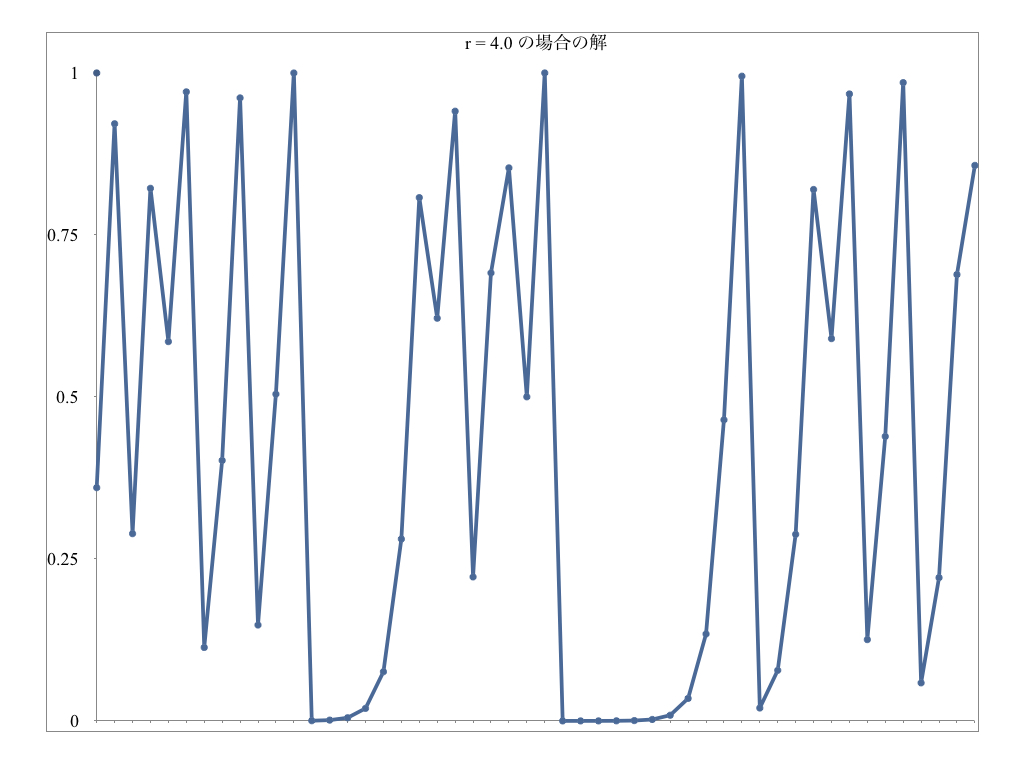
r=4.0の場合は、個体数の変動に規則性は見られず、もはや予測不能となります。
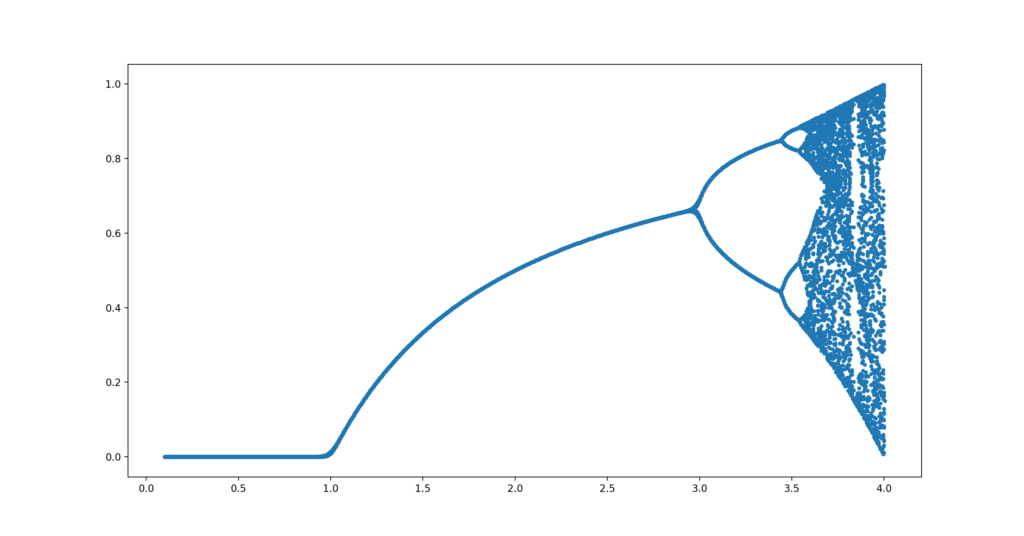
ここで、rと個体数の関係を散布図で示したのが、以下の分布図です。VBAで、簡易的に、rは0.1刻み、世代数は50までで計算しましたが、傾向がかなり掴めます。
rが小さいうちは、絶滅ルートを辿りますが、rが大きくなるにつれて、定常的になり、rがさらに大きくなると、個体数の変動が複雑になっていく様子がわかります。
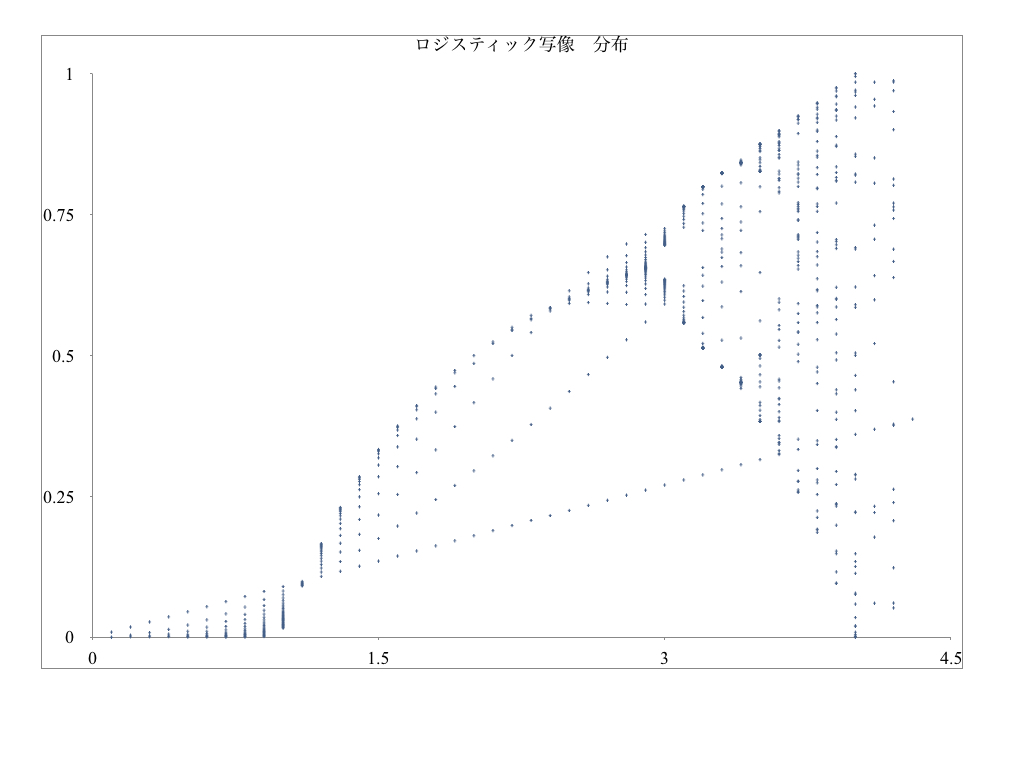
気象学でよく出てくるバタフライ効果がよくわかる事象でもあります。
バタフライ効果は、例えば上海で蝶々が羽ばたきをするとアメリカで竜巻が起きるといった表現がなされます。初期状態の微細な変化が後々に大きな変化となって現れます。
このような複雑系の現象が、このような極めて簡単な方程式から導くことができます。
以下がPythonで書いたコードです。刻み幅rplusを細かくすればさらに細密になります。
import math
import matplotlib.pyplot as plt
rplus=0.005#パラメータ刻み幅
r=0.1#パラメータ初期値
x = []
y = []
while r<4.2:
xn=0.1
for i in range(300):
xn=r*xn*(1-xn)
if(r>2.8) and (r<4.1):
if i>58 :
if(xn>=0.2) and (xn<=1.0):
x.append(r)
y.append(xn)
r+=rplus
plt.scatter(x,y,marker=".")
plt.show()